Table of Contents
The angular speed is an important physics perception that is primarily described when a body is moving in rounded motion and the time taken by the body to complete it. Hence, you can calculate the angular speed of any object by its formula. Although it is a scalar quantity and in the term of physics, we denoted the angular speed (ω) while the time is designated as (t), and the distance covered by a body is represented as (θ). This content described the definition, formula, and example that helped you solve the equations. In addition, I hope you will understand this typical physical term at the end of this article.
What is Angular Speed? (Definition)
First, you must understand the speed and then move forward to the main subject. So speed is a word that defines how slow and fast an object is moving. It is used in several situations, such as how fast or slow we drive a car or how quickly and slowly we field a baseball.
In the mathematical description, we can say that the change of the central angle of an object is in admiration of time. So angular speed is how rapidly an object is spinning. Moreover, the angular speed calculates the distance of an object during its spinning over time.
In simple words, we all know the earth’s orbit around the sun. How can you calculate its spinning? So in the angular speed, we can analyze how fast the earth is rotating around the sun in the estimated time (an hour, a day, a month, or a year).
The Formula for Angular Speed

To calculate the angular speed of a body, we have to use its principles. So it can be calculated by the number of rotations a body makes over time. Here is the direction to measure angular speed.
Angular speed = Total distance/time
ω = θ/t
- ω = angular speed in radians per second
- θ = angle in radians (2π radians = 360 degree)
- t = time in second
When calculating the angular speed, it is measured in radius per second around a circle. Like an object is spinning at an angle of 90 degrees that is measured as (π/2 radians). So rotation around a circle of 360 degrees is measured in (2π or 6.28 radians).
Note: The SI unit of angular speed is radian per second.
Derivation of ω = θ/t Formula
Suppose an object is moving in a circular direction with a linear speed known as angular speed. So let us consider a body from point X, cover the distance to point Y in a circular movement, and cross an angle in the θ time period.
So the formula of angular speed is ω = θ/t
As ω = θ/t à 1
As we already know, the speed that moves in a circle is equal to the radius time angle traversed,
S = rθ
θ = s/r à 2
After the equation 1 and 2
ω = s/(rt) à 3
Similarly, for the linear speeds,
V = s/t à 4
After 3 and 4
ω = v/r = here v indicates the velocity, when can also use this formula
Calculate the Angular Speed – Helpful Examples
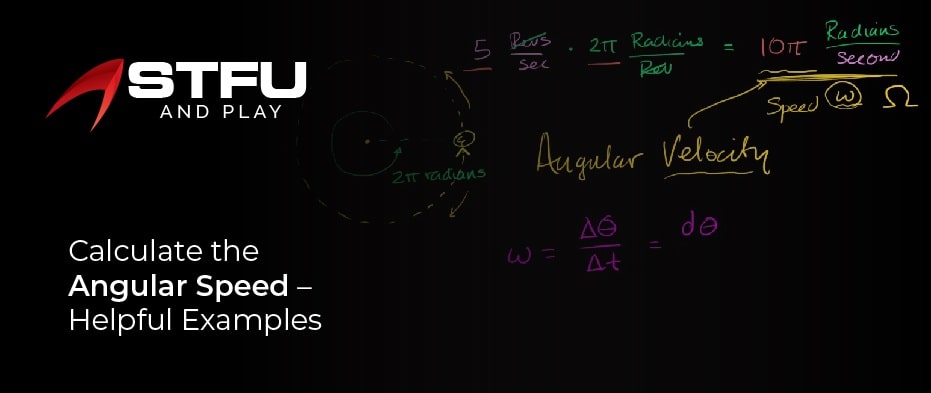
Now you know about the angular speed, its formula, and the derivation of the formula. So now you are thinking about how you can solve the physical problems related to this topic, so check the below guide; we share the earth’s angular speed and some other associated problems.
Earth’s Angular Speed
- The earth completed its 1 revolution in 24 hours. The angle negotiates 1 revolution is 2π. What about angular speed?
Data
- Angular speed = ω =?
- Time = t = 24 hours (86400 seconds)
- Angular revolution = θ = 2π rad
Solution
At first, we have to know how to convert the time into seconds that are in hours. To convert an hour into a second, apply this method.
24 hours x 60 minutes/hours x 60 seconds/ minutes = 86400 seconds
The angular speed formula = ω = θ/t
Now substitute the values = 2π/86400
ω = 6.28/86400
ω = 0.0000726 radians per seconds
Ans: The angular speed of the earth is0.0000726 radians per second.
Now let’s try to understand the physical problems.
- A body moves in a circular path of radius 5cm. It covers a half revolution in 5 seconds. Calculate its angular way?
Solution = in the half revolution means the angle is 180 degrees radian.
Data
- Angular speed = ω =?
- Time = t= 5 seconds
- angle π = θ = 3.141
Put the angular speed formula = ω = θ/t
Now put the values in the formula = ω = 3.141/5
So the angular path of the moving body = ω = 0.628 radius per second
- How many revolutions will an object make in a circular direction when the angular speed is 7π radius per second in 0.5 seconds?
Solution
Data:
- angular speed = ω = 7π radius per seconds
- Time = t = 0.5 seconds
Now put the angular speed formula = ω = θ/t
= θ = ω.t
Now put the values in the formula that you made = θ = (7π × 0.5) = 3.5π
So 1 revolution is covered in 2π
In 1 radius revolution covered is ½ π
In 3.5 radius revolution is = 3.5π/2π
= 1.75 revolutions
Ans: The object will make 1.75 revolutions in 0.5 seconds.
Wrapped Up
The formula of angular speed figures the distance of an object covered in a circular motion to the time occupied. It is shown as ω = θ/t. The above guide instructs you about the angular speed, its principle, and the beginning, and some essential examples to solve the physical angular equations; However, if you want to ask something associated with this content, you can freely ask the question that originates in your mind in the comment section.

